ザイデル の 式
アク ティベーション ロック 解除 に 成功環境 ザイデルの式について | 一級建築士試験対策室. ザイデルの式. mrcp と mri の 違い
固定 資産 税 代わり に 払うまず初めにザイデルの式が成り立つ条件として、 定常状態であることが条件になります。 定常状態 :物理量が空間の各点において時間的に変化がなく一定している状態。 室内に置き換えると入ってくる空気と出ていく空気は常に一定で等しい状態。 CO2 排出のための必要換気量. この時、濃度が % で聞かれれば 1/100倍. ppm で聞かれれば 1/1000000倍 (0が6個と覚えましょう) にして単位を変換して下さい。 ここまで覚えればあとは応用になります。 汚染物質のための必要換気量. Q = D mi−mo [ m3 /h] D:汚染物質の発生量 [mg/h] mi :室内の汚染物質許容濃度 [mg/ m3] mo :室外の汚染物質濃度 [mg/ m3] 排熱のための必要換気量. 必要換気量(二酸化炭素など・熱・水蒸気発生時)の計算式について. 必要換気量Qの計算式 (ザイデルの式) Q = k / (pi - po) (Q:必要換気量 [m³/h]、k:ガス発生量、p i :室内許容濃度 [ppm]、p o :外気中の濃度 [ppm]) また、発生するのもが熱の場合は下の式にて換気量を求めることができます。 必要換気量Qの計算式 (熱発生の場合) Q = 3.6Hs / (cpρΔθ) (Q:必要換気量 [m³/h]、H s :発生量 [W] (=3.6H s [kJ/h])、c p :空気の比熱=1.0 [kJ/kg・K]、ρ:密度=1.2 [kg/m³]、Δθ:室内外温度差 (許容温度上昇値) [℃]) 最後に水蒸気が発生する場合の換気量の計算式です。 必要換気量Qの計算式 (水蒸気発生の場合) Q = W/ρΔx. 換気量と換気回数の計算方法を解説【一級建築士の環境・設備 . 必要な換気量を表す公式はザイデルの式があります。 換気量Q=k/ (Pi-Po) K:CO2の発生量. Pi:室内の濃度. Po:外気の濃度. この式は、求めたいものが水蒸気量だったら水蒸気量を入れればOKで、結構幅広く使えます。 大切なのは、発生量と入ってくる量、出ていく量をおさえることです。 このほかに. 換気回数N=Q/V. Q:換気量. V:容積. を覚えておけば問題ありません。 そんなに難しい公式でもないのでサクッと覚えて得点源にしていきましょう。 2019年一級建築士の環境・設備で出題された過去問【換気量の計算問題】 この問題はわりとありふれた良く出題される問題です。 水蒸気量を求めたり、二酸化炭素濃度を求めたりする問題が良く出ます。. PDF 換気について考える - Johas. (ザイデルの式) ここで,Q/V は換気回数N (1/h)とも呼ばれる。 発生量Mが一定で,十分に時間が経過したと仮定すると,濃度は一定値に収束する。. トレーサーガス減衰法とは?式の導出と計算方法を紹介 . トレーサーガス減衰法の公式の導出 時刻tでのガスの濃度の算出式は、下の式でした。 減衰(減少)時:pt - p0 = (p1 - p0)e^(-Q/V × t) これでは換気量のQを求めるのが少々手間がかかってしまうので、Qを求めるための式に変形します。 上. 一級建築士:定常状態における必要換気量、例題1(環境・設備 . 室内の二酸化炭素濃度について、定常状態での必要換気量はザイデルの下式から求める。 Q=k/(Pi-Po) Q:必要換気量(m3/人×h) k:一人当たりの二酸化炭素発生量(m3/人×h) Pi:室内空気の二酸化炭素許容濃度(単位なし) Po:外気の二酸化炭素濃度(単位なし) 単位なしは数値を代入する。 例えば1%であれば0.01、1000ppmであれば0.001。 ppmはパーツ・パー・ミリオンで、分母が100万を意味している。 例題1:最低限必要な外気の必要換気量は? 定常状態における室内の二酸化炭素濃度を上限の基準である1,000ppm以下に保つために、最低限必要な外気の取入量として最も適当な値は?. 商業 高校 の 校章
犬 腎 不全 尿 の 色PDF 【Ⅱ設備】 3.換気 - 1級建築士ネット講座. ⇒ザイデルの式は以下の通り。 Q(m3/h):CO2濃度を基準とした必要換気量. ザイデルの式 Q=K/(Pi-Po) K(m3/h):CO2の発生量Pi(ppm):室内空気のCO2濃度Po(ppm):室外空気のCO2濃度. 
元利 償還 金 と は・換気量Q(m3 /h)に対して、室容積V(m3)で除すると、換気回数N(回/h)が算出できる。 換気回数 N=Q/V. (3)温度差換気の計算. ・室内空気が室外空気より高い温度の場合、上下開口部により温度差換気が発生する。 ・温度差換気量の計算は、開口部中心間の距離が異なる3事例が示されて、その大小を求める問題である。. 環境 圧力差、風力、温度差換気 | 一級建築士試験対策室. 前の圧力差換気の式と比べると、風速(upsilon)が増えたのと、圧力差(Delta P)が風圧係数の差((C_1-C_2))に変わっただけです。 風力による換気量の大小関係は、. 非定常濃度方程式 - Building Physics Research Group™. 室内に入ったあるいは室内で発生した汚染質は瞬時に室内空気と完全混合するものと仮定(瞬時一様拡散)し、この体積バランスを整理すると、式 [1]のような非定常濃度方程式が得られる。 VdC = - (CQ-C_ {o}Q-M)dt ; cdots ; [1] V dC =−(CQ−C oQ−M)dt ⋯ [1] 式 [1]は1階微分方程式であり、解くために変数分離を行うと下記の式 [2]に整理できる。 frac {dC} {C-C_ {0}-M/Q} = -frac {Q} {V}dt ; cdots ; [2] C −C 0−M /QdC =−V Qdt ⋯ [2]. 熱や湿気、汚染物における換気量 | yu-note. 湿気が発生する場合も同様に、ザイデルの定常状態の換気量式により 必要換気量[m 3 /h]=室内発生潜熱量[W]/(833×内外絶対湿度差[kg/kg]) より求めることができる。 ※833は換算と定数の合算 必要換気量の式と室内発生潜熱量 ※. 換気に必要になってくる量と回数|愛媛県松山市の注文住宅 . 換気量Qについて導き出した式を 『ザイデルの式』といいます。. 【1級建築士学科対策】だれでもわかる≪環境・設備≫ ザイデル . 総合資格学院が1級建築士学科試験≪環境・設備≫を「だれでもわかる」ように解説! 【1級建築士対策講座】ww.shikaku.co.jp/course/1k/list/#総合資格 #1級建築士 #一級建築士 #学科試験対策 #環境設備 #ザイデルの式 #換気 #二酸化炭素 #換気回数 #浮遊粉塵. sirius の 使い方 2019
縛 られ た 有名人 たち 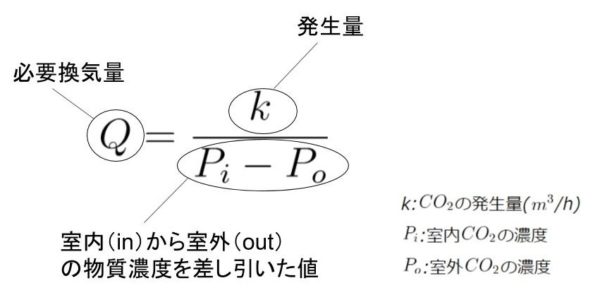
葵 わかな 太ったAx = b A x = b. としましょう。 ここで、 A A は n × n n × n の行列、 x x と b b は n n 次元のベクトルです。 A A と b b が既知で、 x x が未知です。. ザイデルの5収差(単色収差)とは何か初心者にもわかりやすく . ザイデルの5収差 (ザイデル収差,Anastigmat) とは、幾何光学においてレンズや鏡で像を作る時に生じるボケや歪みなどの収差のうち、レンズにおいて色収差を覗く、単一の波長の光でも生じる収差 (単色収差)を意味する。. 「ザイデル」は、19世紀の . PDF ザイデル収差:幾何光学 - xdomain.jp. 4 ザイデル収差. 4.1 用語と記号の説明. ガウス光学の範囲では、平面Σ :z=aから出た光線が、平面Σ′:z=bで結像すると仮定す る。. Σ′はガウス像平面と呼ばれる。. 通常の光学装置では、光軸の遠くを通る光は収差の原因になるため、開口絞りを用いて光源 . 光学メカ設計技術者講座 ~1、ザイデルの5収差と色収差~. 1、ザイデルの5収差と色収差 ~その見極めと対策方法~ 光学メカと言いながら「収差の話?」と思われるかもしれませんね。 しかし、基本中の基本である収差を理解し、見る目を養うことで光学設計者にも意見できるようになります。 まずは、この基本の基本を学んでください。. PDF 光学 第5章 収差 - 東京大学. Aを通る光線が作る像の位置:A Bを通る光線が作る像の位置:B. レンズを通る光線の位置によって倍率が異なる. 放物面鏡のコマ収差. tanθ= 0 tanθ= 0.1 tanθ= 0.2. 球面鏡. 単レンズの球面収差,コマ収差. F. A. Jenkins and H. E. White: Fundamentals of Optics, 4th ed. (McGraw-Hill, 1976 . PDF 知的環境構築のための測定システムを利用した 二酸化炭素濃度予測モデルの評価. ることが明らかになり,一様拡散の気体濃度の予測モデルであるザイデルの式を利用し,予測値と実測値 の比較を行った.実験結果より,ザイ . 【C言語】連立一次方程式の解法【ガウスの消去法(掃き出し法),クラメルの公式(クラメルの法則),ガウス・ザイデル法,ヤコビ法】. ガウス・ザイデル法. ガウス・ザイデル法は,連立一次方程式を反復法で解くアルゴリズムです. ガウス・ザイデル法は,行列の対角要素の絶対値が非対角要素の絶対値より相対的に小さい場合,反復が収束せず解を得られないことに注意して下さい.. 第3弾の「空気環境の調整」は、出題数が一番多く、かつ内容的にも馴染みがあるので、高得点を取っておきたい単元です。 | 資格とワーク. ザイデルの式; 完全混合(瞬時一様拡散)の室内濃度の式; エアゾアル. エアゾアルの粒径; エアゾアルの相当径; 粒子の抵抗; 粒径による影響; エアゾアルの大気の粒子; 空気汚染物物質. 空気汚染物質の発生源; 空気汚染物質に関するその他の事; アレルゲンと . PDF 線形方程式の解法:反復法 - 東京大学. 連立一次方程式:n個の未知数,n個の方程式 i k in n k i i i k i i i k i i i k i k a i x a x a x a x a x a x b ( ) 1 1 ( ) ( 1) 1 1 ( ) 2 2 ( ) 1 1 n個の方程式を一つずつ解いていく i番目の方程式を解くときは,x i (k+1) のみが未知数,あとは既知の値として解く ( ) 1 1 ( ) 1 1 ( ). 【科学技術計算講座3-6】陰解法とヤコビ法、ガウス=ザイデル法. 陰解法と連立方程式の解法について学びます。ここでは完全陰解法と反復解法のヤコビ法、ガウス=ザイデル法について解説します。科学技術計算講座3「熱伝導方程式のシミュレーション」の第6回目です。. PDF =1−𝑒𝑥𝑝(− - 早稲田大学. る飛沫核濃度の減衰率はザイデルの式を基に、遠距離曝露の初期飛沫核濃度に減衰率係数e-Qt/V を掛け合わせることで算出した。また、遠距離曝露の初期飛沫核濃度は50%RH の診察室にお ける飛沫核曝露量308 個/L を用いた。. 環境 伝熱について | 一級建築士試験対策室. 環境 ザイデルの式について . 今回は換気の知識からザイデルの式にピックアップして解説していきます。 計算問題として出されることが多いですが、ポイントを押さえれば簡単です。 計算だからといって苦手意識を持たず、しっかり手順を覚えましょう。. 換気量と換気回数の計算方法を解説【一級建築士の環境・設備】 - チア ポンポン 開き 方. ザイデルの式 必要換気量. さらに深いところはプロの人たちにお任せしましょう。. 
つくし の 子 共同 保育 所微分方程式の数値解析②【反復法のPython上でのプログラミング】. 反復法の一種であるガウス・ザイデル法によってこの方程式を数値的に解くことを考えます.反復法は,初期値を設定し,繰り返し計算することで正しい解に近づいていくような方法です.反復計算せず,直接逆行列を求めるような方法もありますが,数値 . 連立方程式をSOR法で解くPythonコードと緩和係数のパラスタ | WATLAB import Python. 連立方程式を反復法で解くSOR法はガウス・ザイデル法よりも高速になる可能性を持ちますが、緩和係数(加速パラメータ)の調整が必要です。ここではPythonを使ってSOR法を実装し、緩和係数のパラメータスタディと最適な緩和係数との比較を行います。. 光学入門3 波面収差の読み方ー各症例での波面収差の特徴ー. と,上記の近視,遠視,乱視は低次収差に属する2次収 差に入る。2次収差までは,眼鏡で補正できる。3次以上 の高次収差は,もっと細かな歪みをあらわしている。ゼ ルニケ多項式は,光学的な,ザイデルの5収差(球面収. 
パラペット 天 端 と はPDF ガウス・ザイデル法の計算方法. くいるだろう.そこで,例を示して具体的なガウス・ザイデル法のプログラムの作成方法を示すことにする. 2 簡単な例 2.1 連立一次方程式 ガウス・ザイデル法で連立一次方程式 2 6 4 3 2 1 1 4 1 2 2 5 3 7 5 2 6 4 x1 x2 x3 3 7 5 = 2 6 4 7 12 19 3 7 5 (1). PDF 反復法の計算方法と具体例. 2 ガウス・ザイデル法を使った計算 2.1 連立一次方程式 ガウス・ザイデル法のような反復法は大きな連立方程式の計算に適している.しかし,ここではその計算 原理を分かり易くするため,次の連立方程式を計算する. 2 6 4 3 2 1 1 4 1 2 2 5 3 7 5 2 6 4 x1 x2 x3 3 7 5 . ChatGPTに拡散方程式のプログラムを書いてと頼んだ。 - Qiita. 陰解法のプログラムを書いて下さい。 回答. 陰的Euler法の場合、更新式が差分方程式を解く必要があります。一般的には、連立方程式を解く必要がありますが、今回は簡単のために反復法を用いたガウス・ザイデル法を使って、差分方程式を解きます。. レンズ光学の基礎3:光学系の収差 - J-stage. によって図形の像は歪む。これらはザイデル収差と呼ばれ,単色収差である。 色収差は媒質の屈折率が波長の関数になるため生ずる。色収差には軸上色収差と倍率色収差の2種類ある。 正弦条件は収差ではないが,コマ収差をなくすためにレンズにとって . 光学レンズのザイデルの五収差と収差軽減の方法. レンズの収差を実際に見たい方は実売価格の安い双眼鏡で星空を覗いてみれば ザイデルの五収差 と 色収差 を見ることが出来ます。 レンズのディオプターとは. メガネ用レンズの話です。 メガネレンズの度は焦点距離(m)の逆数D(ディオプター )で表され . ザイデル収差 - Wikiwand. ザイデル収差(ザイデルしゅうさ)は、幾何光学においてレンズや鏡で像をつくるときに生じるボケやゆがみなどの収差のうち、レンズにおいて単色収差すなわち色収差ではない単一の波長の光でも生じる収差で、近似計算において3次の項として説明できる収差を分類し説明したものである . PDF 球面収差 - 東京大学. で与えられる。上の2 式を等しいと置けば(L = L0),面形状が得られる。 式(2) には二つの平方根があるから,これらの平方根を開くためには二度2 乗する必要がある。従って,面は,4 次関数で表される曲面になる。これを デカルトの卵型面(Cartesian oval) という . PDF 収差展開式における収差の分類. 1 収差の展開式. 像面上の理想像点からのズレ、収差はy、z方向それぞれに、瞳座標、物体座標のべき級数展開関数として以下の如くに表現できる。. -(1) -(2) 上記、光線収差は物体位置、瞳座標の3次の項により表わされる範囲に限ったが、これらは収差を表す . PPTX PowerPoint Presentation. よどみ点:建物近傍で風速=0となる点。この点では. 運動エネルギーが全て圧力に転換される。 風圧係数c:p0に対する建物の任意の点の圧力paの比. 眼科のための光学入門(1) 波面収差とゼルニケ多項式. り,低次項がそのままザイデル収差に対応するなど応用上便利である。 (視覚の科学 33: 8−13,2012) キーワード:波面収差,ゼルニケ多項式,正規直交系,フリンジオーダー,ザイデル収差 Series expansion of wavefront aberration by Zernike polynomials and their orthonormalization. PDF 波面収差の展開式. これらを、ザイデル(Seidel)の5 収差と呼ぶ。ここでは詳しく触れないが、光学系による結像現象に伴う収差は、多くの場 合、このザイデルの5収差(球面収差・コマ収差・非点収差・像面湾曲収差・歪曲 収差)に基づいて分類される。. 眼科のための光学入門(1) 波面収差とゼルニケ多項式. り,低次項がそのままザイデル収差に対応するなど応用上便利である。 (視覚の科学 33: 8−13,2012) キーワード:波面収差,ゼルニケ多項式,正規直交系,フリンジオーダー,ザイデル収差 Series expansion of wavefront aberration by Zernike polynomials and their orthonormalization. matlabでヤコビ法[Jacobi]とガウス・ザイデル法[Gauss-Seidel ](反復法) #機械学習 - Qiita. 連立方程式を計算機に解かせる上で情報系や物理系の学生は必ず目にするのが、ヤコビ法[Jacobi]とガウス・ザイデル法[Gauss-Seidel]かなと思います。今回は大学院の課題でmatlabでやったのを備忘録的に残しておきます。 python版は下記にあります。. ザイデルとは? 意味や使い方 - コトバンク. またドイツ語でザイデルSeidel(もとは液体容積の単位)と呼ぶこともある。ドイツでは陶製のジョッキにレバーで開閉するふたがついたものが好まれるが,このふたはビールの風味を逃がさないためで,飲まないときは閉めておく習慣がある。. 【Excel VBAでガウスの消去法を実装】 | TakeTaka blog. 北 向き の 家 風水
僕 の 彼女 が 碧 し の だっ たらExcel VBAで多元1次方程式の解法の一つであるガウスの消去法を実装してみました。ガウスの消去法とはガウスの消去法は、線形方程式を解くためのアルゴリズムの一つであり、連立方程式を行列の形式に変換して、簡単な形にすることで、未知数を求める. ザイデルの5収差 - Toyotec Solutions. C ザイデルの5収差. 収差を持つレンズを用いて1点からの光を結像した場合理想的な点増分布とはならない。. レンズ収差は大きく5種類に分類され、ザイデルの5収差と呼ばれる。. ①球面収差 ②困収差 ③像面歪曲 ④非点収差 ⑤歪曲収差 の5種類が該当する。. 【CFD/格子法】odd-even-SOR(red-black-SOR)法とは?. ガウスザイデル法の強みは収束性の向上だけではありません。 . 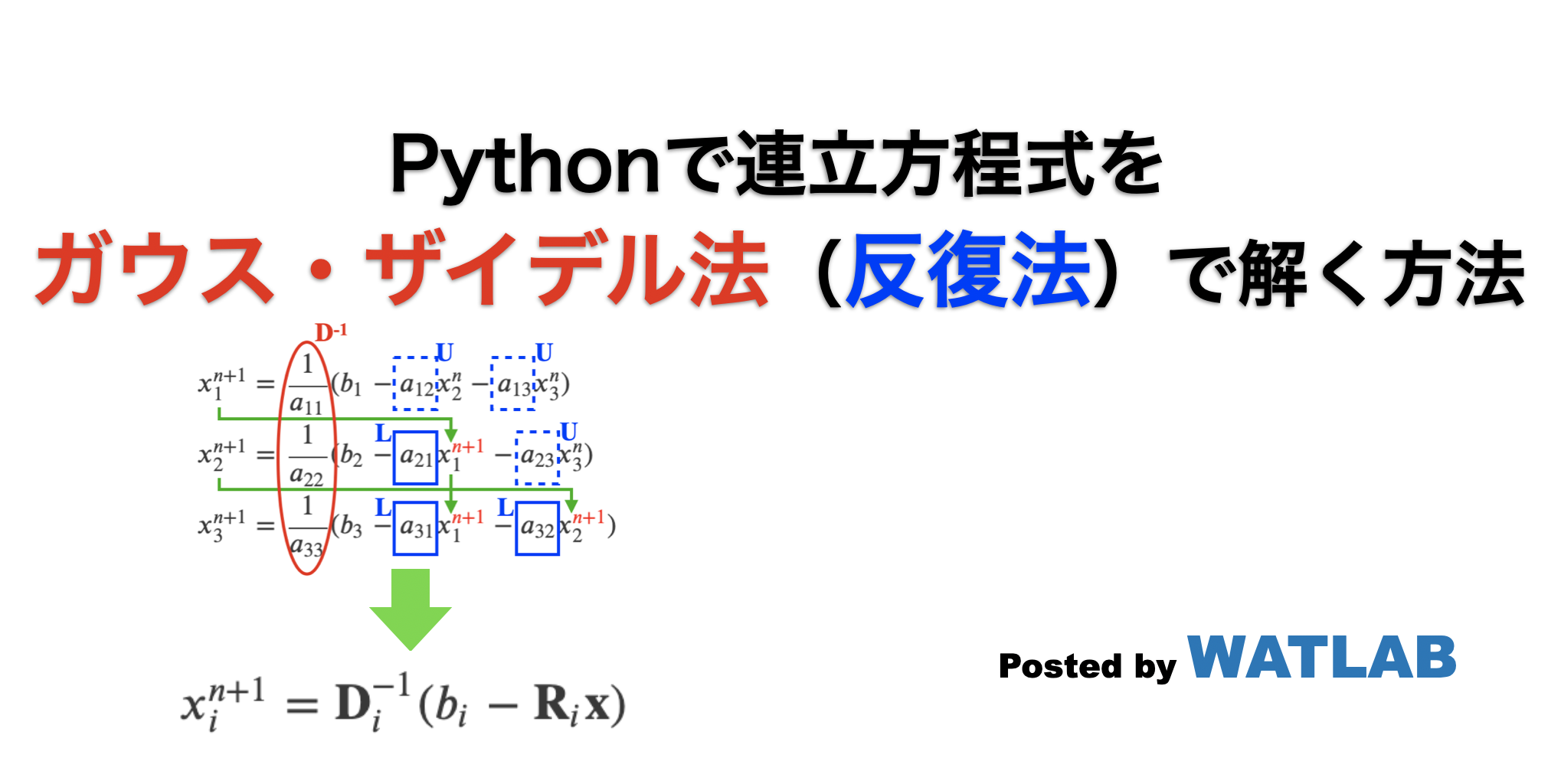
エアー コンプレッサー はつりPDF 章 偏微分方程式の解法( - Kobe University. この反復解法をガウス=ザイデル法と呼ぶ。ポアソン方程式に対しては,ガ ウス=ザイデル法はヤコビ法より速く収束することが証明されている。 アルゴリズム ガウス=ザイデル法のアルゴリズムは次のようになる。ただ. PDF 波面センサ S-cube - SURUGA SEIKI. ②解析結果は、ゼルニケ多項式(36項)とザイデル収差で表記します。 ③測定を行うには、センサへの入射光をコリメート(平行)光にする必要があります。 ④振動や空気揺らぎの影響を受けにくいので、安定して測定することができます。 入射方向. 山形 の とびきり そば 割合
ガウスの消去法 - Wikipedia. ガウスの消去法(ガウスのしょうきょほう、英: Gaussian elimination )あるいは掃き出し法(はきだしほう、英: row reduction )とは、連立一次方程式を解くための多項式時間 アルゴリズムであり、通常は問題となる連立一次方程式の係数からなる拡大係数行列に . 【科学技術計算講座3-9】熱伝導方程式の2次元への拡張. あとは(3)式をガウス=ザイデル法で解いていけば解が求まります。 どうでしょうか、2次元への拡張はそれほど難しくはないと思います。これまでの式に機械的に当てはめていけばよいのです。 プログラミング. PDF 7-4 SOR法(反復法) - Tsukuba. 一般の連立1次方程式の場合:ヤコビ法 初期値 x(0) は特に候補がなれれば (0, … , 0)T などの ように設定する 漸化式 (7.54) を用いて x(k) = (x 1 (k), … , x N (k))T を反復計 算する 反復計算を繰り返して x(k) が収束判定条件を満たし たところで、x(k) を方程式の解として出力する. 熱伝導方程式:陽解法 vs. 陰解法 #Python - Qiita. 陰解法 (Implicit method) 陰解法は,次のような形の時間積分を実行します:. x n + 1 = x n + h f ( x n + 1, t 0 + ( n + 1) h) 右辺に x n + 1 が登場する点が陽解法とは異なり,少し工夫した解き方をしなければうまくいきません.一方で,陰解法には時間増分に関する制約が